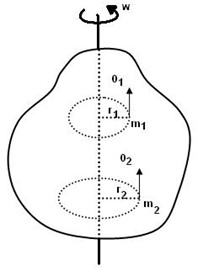
DÖNEN BİR CİSMİN KİNETİK ENERJİSİ
1. AÇISAL HIZ
Yarıçap vektörünün birim zamanda taradığı açıya açısal hız denir. w ile gösterilir. \(\omega = \frac{{2\pi }}{T}\) veya \(\omega = 2\pi f\) formülü ile bulunur.
2. ÇİZGİSEL HIZ
Düzgün dairesel hareket yapan bir cismin daire yayı üzerinde birim zamanda aldığı yola çizgisel hız denir. V ile gösterilir. Birim m/s’dir. \(v = \frac{{2\pi r}}{t} = 2\pi fr\)
PERİYOT: Düzgün dairesel hareketin bir tam devir yapılması için geçen zamana denir.T ile gösterilir. Birimi S’dir.
FREKANS: Düzgün dairesel hareket yapan bir cismin birim zamandaki devir (dönme) sayısına denir. f ile gösterilir. Birimi 1/S yada Hz’dir. Periyotta Frekans arasında T.f=1 bağıntısı vardır. \(T = \frac{1}{f}\) periyot \(f = \frac{1}{T}\) frekans
Çizgisel hız ile açısal hız arasında \(v = \omega r\) bağıntısı vardır. Bir eksen etrafında dönebilen cisimler kuvvet uygulanıp döndürüldüğünde Cismi Oluşturan tanecikler yol almış olur. Kuvvet bir iş yapar ve bu iş cisme enerji olarak aktarılır. Cismin sahip olduğu enerji dönme kinetik enerjisidir.
Dönen bir cismin kinetik enerjisi \({E_K} = \frac{1}{2}.I.{\omega ^2}\) burada I cismin eylemsizlik torku (cismin dönme eksenine göre eylemsizlik momenti) olup \(\sum {m{r^2}} \) dir. Yani dönen bir cismin kinetik enerjisi \({E_K} = \frac{1}{2}.{\omega ^2}.\sum {m{r^2}} \) şeklindedir. Sonuç olarak;
- Yalnız dönme hareketi yapan cismin kinetik enerjisi \({E_K} = \frac{1}{2}.I.{\omega ^2}\)
- Yalnız öteleme hareketi yapan cismin kinetik enerjisi \({E_K} = \frac{1}{2}m{v^2}\)
- Dönerek ilerleyen cismin toplam kinetik enerjisi \({E_K} = \frac{1}{2}m{v^2} + \frac{1}{2}I{\omega ^2}\)
Sabit bir kuvvet büyüklüğü değişmeyen hız vektörüne sürekli ve dik etki ederse cisme r yarıçaplı çember üzerinde düzgün dönme hareketi yaptırır. Bu harekete düzgün dairesel hareket denir.