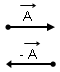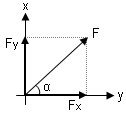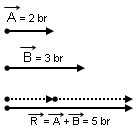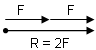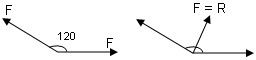Eşya ve olayları tanımlarken iki tür büyüklük kullanırız.
–Skaler büyüklükler
–Vektörel büyüklükler
Skaler büyüklükler: Sadece sayı ile ifade edilen büyüklüklerdir.
Örnek: 10 kalem, 20 m, 60 saniye v.b.
Vektörel büyüklükler: Sadece sayı ile ifade edilemeyen,
Doğrultusu
Yönü
Şiddeti ( Büyüklüğü )
Uygulama noktası ( Başlangıç noktası ) bilinen büyüklüklere denir. Vektörel büyüklükler “Vektör” ile gösterilir.
Bir A vektörü, \(\overrightarrow A \) ile, büyüklüğü de \(\left| {\overrightarrow A } \right|\) ile gösterilir.
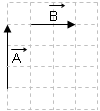
Şekildeki vektör için;
Doğrultusu ………………xy
Yönü …………………….. K’dan M’ye doğru
Şiddeti ………………….. 2 birim
Uygulama noktası …….. K
Vektörlerin özellikleri:
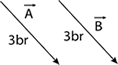
1.) İki vektörün toplamı ya da farkı yine bir vektördür.
\(\begin{array}{l}\overrightarrow A + \overrightarrow B = \overrightarrow C \\\overrightarrow A – \overrightarrow B = \overrightarrow D \end{array}\)
2.) Vektörlerde toplamada değişme özelliği vardır.
\(\overrightarrow A + \overrightarrow B = \overrightarrow B + \overrightarrow A \)
3.) Bir vektörü skaler bir sayıyla çarpmak ya da bölmek o vektörün büyüklüğünü çarpmak ya da bölmek demektir.
4.) Bir vektörün zıt işaretlisi, zıt yönlü bir vektördür. Doğrultusu değişmez.
5.) Bir vektörün doğrultusu, yönü ve şiddeti değiştirilmeden istenilen yere taşınabilir.
6.) Doğrultusu, yönü ve şiddeti aynı olan vektörler eşit vektörlerdir. Uygulama noktası (Başlangıç noktası) farklı olabilir.
\(\overrightarrow A = \overrightarrow B \)
Vektörlerin toplanması:
Vektörlerin toplanmasında üç yöntem vardır.
1.) Paralel kenar metodu
2.) Ucuca ekleme metodu
3.) Bileşenlere ayırma metodu
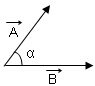
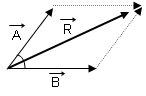
1.) Paralel kenar metodu
Başlangıç noktası aynı olan vektörler paralel kenara tamamlanır. Başlangıç noktası ile kesim noktasını birleştiren vektör, toplam vektörü verir.
\(\overrightarrow R = \overrightarrow A + \overrightarrow B \)
Cosinüs Teoremi:
\({R^2} = {A^2} + {B^2} – 2 \cdot A \cdot B \cdot Cos\alpha \)
İkiden fazla vektörün toplanması paralel kenar metoduna göre yapılırken önce rasgele iki vektörün toplamı yapılır, sonra toplam vektör ile diğer vektör paralel kenar metoduna göre yapılarak işlem devam ettirilir.
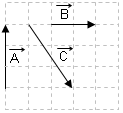
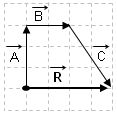
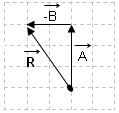
2.) Ucuca ekleme metodu:
Vektörlerden biri rasgele seçilip diğer vektörlerin doğrultusu, yönü ve şiddeti değiştirilmeden sıra ile ucuca eklenir. Birinci vektörün başlangıç noktası ile son vektörün ucuna doğru toplam vektör çizilir.
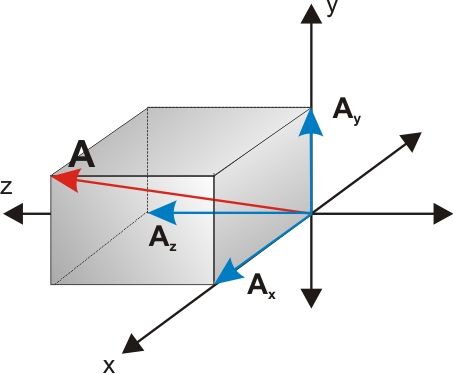
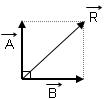
3.) Bileşenlere ayırma:
Bir vektörün bileşenleri o vektörün x ve y düzlemlerindeki izdüşümüdür.
\(\begin{array}{l}\overrightarrow F = \overrightarrow {{F_X}} + \overrightarrow {{F_Y}} \\{F_X} = F \cdot Cos\alpha \\{F_Y} = F \cdot Sin\alpha \end{array}\)
Vektörlerin çıkarılması:
İki vektör arasındaki çıkarma işlemi bir vektör ile diğer vektörün zıt işaretlisinin toplamı şeklinde ifade edilir.
\(\overrightarrow R = \overrightarrow A – \overrightarrow B \)
ÖZEL DURUMLAR :
1.) İki vektör arasındaki açı sıfır ise yani paralel ise ve aynı yönlü ise toplam vektör, vektörlerin cebirsel toplamına eşittir.
2.) İki vektör arasındaki açı 180o ise yani yönleri zıt ise toplam vektör cebirsel farka eşit olur.
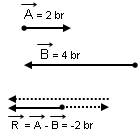
3.) İki vektör arasındaki açı 90 ise toplam vektör pisagor bağıntısından bulunur.
4.) İki vektörün toplamı, vektörlerin büyüklüklerinin cebirsel toplamından daha büyük, cebirsel farkından daha küçük olamaz.
\(A – B \le R \le A + B\)
5.) Aralarında a açısı bulunan iki kuvvet eşitse bileşke vektör açıortay üzerindedir.
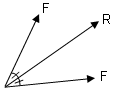
6.) Aralarında a açısı bulunan iki kuvvetin bileşkesi büyük olan kuvvete daha yakındır.
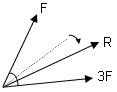
EŞİT ŞİDDETLİ VEKTÖRLERDE ÖZEL DURUMLAR :
1.) \(\alpha = 0 \Rightarrow R = 2F\)
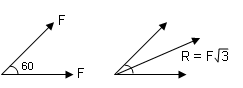
2.) \(\alpha = {60^o} \Rightarrow R = F\sqrt 3 \)
3.) \(\alpha = {90^o} \Rightarrow R = F\sqrt 2 \)
4.) \(\alpha = {120^o} \Rightarrow R = F\)
5.) \(\alpha = {180^o} \Rightarrow R = 0\)