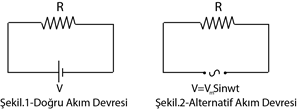
Periyodik olarak yönü ve büyüklüğü değişen akımlara alternatif akım denir.
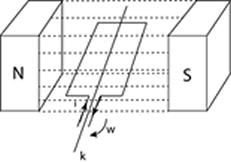
İletken bir tel manyetik alan içinde k ekseni etrafında w açısal hızıyla döndürülürse, manyetik akı sürekli değişeceğinden, telden geçen akımın yönü ve büyüklüğü de değişecektir.
Şekildeki tel çerçevenin alanı A olsun;
Çerçevenin içinden geçen manyetik akı;
\(\phi = B.A.Cos\theta \)
Eğer çerçeve N sarımdan oluşuyorsa;
\(\phi = N.B.A.Cos\theta \)
r. Burada θnda çerçeve normalinin manyetik alan çizgileriyle yaptığı açıdır.
Çerçeve w açısal hızıyla t süre döndürülürse ve bu arada kadar açı taradığı varsayılırsa;
\(\theta = w.t\)
yazılır.
\(\phi = N.B.A.Cos\theta \) olduğundan
\(\phi = N.B.A.Coswt\) yazılır.
Çerçevede açığa çıkan emk ise;
\(\varepsilon = – \frac{{\Delta \phi }}{{\Delta t}}\) ile bulunur. Bu ifade manyetik akının zamana göre türevi anlamına geldiğinden;
\(\varepsilon = NBAwCoswt\) halini alır.
Maksimum emk’yı bulmak demek Coswt=1 demektir.
Buradan \({\varepsilon _{\max }} = NBAw\) yazılır.
O halde genel denklem;
\(\varepsilon = {\varepsilon _{\max }}Sinwt\) olur.
Etkin Değerler:
Alternatif akımın ısı bakımından doğru akımdaki eşdeğerine denir.
\({V_e} = \frac{{{V_{\max }}}}{{\sqrt 2 }} = 0,707 \cdot {V_{\max }}\)
\({i_e} = \frac{{{i_{\max }}}}{{\sqrt 2 }} = 0,707 \cdot {i_{\max }}\)
\(R = \frac{{{V_{\max }}}}{{{i_{\max }}}} = \frac{{{V_e}}}{{{i_e}}}\)
Alternatif Akımın etkileri:
1. Alternatif akımın yönü sürekli değiştiğinden elektroliz yapılamaz.
2. Alternatif akımın yönü ve büyüklüğü sürekli değiştiğinden bu akımın oluşturduğu manyetik alanın yönü ve büyüklüğü de sürekli değişir.
3. Alternatif akımla çalışan bir cihazın direnci R olsun, bu dirençten belirli bir t süresinde açığa çıkan ısı enerjisi;
Doğru Akımda direnç üzerinde açığa çıkan ısı enerjisi,
\(\begin{array}{l}W = V \cdot i \cdot t \Rightarrow P = V \cdot i\\W = {i^2} \cdot R \cdot t \Rightarrow P = {i^2} \cdot R\\W = \frac{{{V^2}}}{R} \cdot t \Rightarrow P = \frac{{{V^2}}}{R}\end{array}\)
Alternatif Akımda direnç üzerinde açığa çıkan ısı enerjisi,
\(\begin{array}{l}W = {V_e} \cdot {i_e} \cdot t \Rightarrow P = {V_e} \cdot {i_e}\\W = {i_e}^2 \cdot R \cdot t \Rightarrow P = {i_e}^2 \cdot R\\W = \frac{{{V_e}^2}}{R} \cdot t \Rightarrow P = \frac{{{V_e}^2}}{R}\end{array}\)
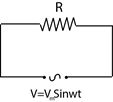
ALTERNATİF AKIM DEVRELERİ
Sadece Dirençli (R) Devre
Sadece R bulunan bir devreye alternatif gerilim uygulandığında;
\(\begin{array}{l}{V_R}{\rm{ = }}{V_m}Sin\omega t\\{i_R}{\rm{ = }}{i_m}Sin\omega t\\{V_e}{\rm{ = }}{i_e}.R\,\,veya\,\,{V_m}{\rm{ = }}{i_m}.R\end{array}\)
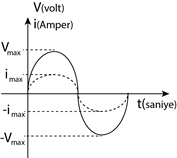
Bu bağlantılardan da anlaşılacağı gibi akım ile gerilim aynı anda maksimum ve aynı anda minimum olmaktadır. Yani aynı fazlıdırlar.
Bobinli (Selfli) Devre
Bir bobinin uçlarına alternatif gerilim uygulanırsa;
\({X_L}\): Bobinin alternatif akıma kaşı gösterdiği dirençtir. Buna indüktif direnç yani indüktans adı verilir. Birimi ohm (\(\Omega \) )
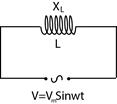

\(\begin{array}{l}{X_L} = \omega \cdot L\\{X_L} = 2 \cdot \pi \cdot f \cdot L\end{array}\)
Grafikten akımla gerilimin aynı fazlı olmadığı t=0 anında gerilimin önde olduğu görülür.
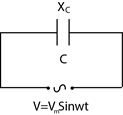
Kondansatörlü (Sığaçlı) Devre:
Bir kondansatörün uçlarına alternatif gerilim uygulanırsa;
\({X_C}\): Kondansatörün alternatif akıma kaşı gösterdiği dirençtir. Buna kapasitif direnç yani kapasitans adı verilir. Birimi ohm (\(\Omega \) )
\(\begin{array}{l}{X_C} = \frac{1}{{\omega \cdot C}}\\{X_L} = \frac{1}{{2 \cdot \pi \cdot f \cdot C}}\end{array}\)
\({V_e}{\rm{ = }}{i_e}.{X_C}\,\,veya\,\,{V_m}{\rm{ = }}{i_m}.{X_C}\)
Grafikten akımla gerilimin aynı fazlı olmadığı t=0 anında akımın önde olduğu görülür.
R-L-C Devresi:
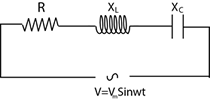
Direnç, bobin ve kondansatörün bir arada bağlanmasıyla elde edilen devreye denir. Direnç, bobin ve kondansatörün alternatif akıma karşı gösterdiği dirence Empedans denir. Z ile gösterilir. Birimi ohm ( \(\Omega \) )
\(\begin{array}{l}{X_L} > {X_C}\\Z = \sqrt {{R^2} + (X_L^2 – X_C^2)} \end{array}\)
\(\begin{array}{l}{X_C} > {X_L}\\Z = \sqrt {{R^2} + (X_C^2 – X_L^2)} \end{array}\)
\(\begin{array}{l}{X_L} = {X_C}\\Z = R\end{array}\)
Bu durumda devre rezonans halindedir. Rezonans halinde devre direnci minimum, akım ve güç maksimumdur.
Rezonans frekansı;
\(\begin{array}{l}{X_L} = {X_C}\\2\pi fL = \frac{1}{{2\pi fC}}\\f = \frac{1}{{2\pi \sqrt {LC} }}\end{array}\)
ile bulunur.