Basit Harmonik Hareket Denklemleri:
\(\begin{array}{l}y = r \cdot Sin\omega t\\v = \omega \cdot r \cdot Cos\omega t\\a = – {\omega ^2} \cdot r \cdot Sin\omega t\\F = – m \cdot {\omega ^2} \cdot r \cdot Sin\omega t\end{array}\)
Uzanım (x):
Cismin herhangi bir andaki denge konumuna olan uzaklığıdır.
* Hareketin İvmesi \( \Rightarrow a{\rm{ = }}\frac{{4{\pi ^2}.x}}{{{T^2}}}{\rm{ = }}{w^2}.x\)
* Hareketi Hızı\( \Rightarrow \vartheta {\rm{ = w}}\sqrt {\left( {{r^2} – {x^2}} \right)} \)
![]()
Basit Harmonik Hareketin Uygulamaları
* Yay Sarkacı:
Hem sürtünmesiz yatay düzlemde hem de düşey düzlemde Basit Harmonik Hareket yapan, yaya bağlanmış, cismin hareketinin periyodu;
Yay Gerilme Kuvveti; F=k.x
\(\begin{array}{*{20}{l}}{F{\rm{ = }}m.a{\rm{ = }}k.x}\\{m\frac{{4{\pi ^2}.x}}{{{T^2}}}{\rm{ = }}k.x}\\\begin{array}{l}{T^2}{\rm{ = }}\frac{{4{\pi ^2}.m}}{k}\\T = 2\pi \sqrt {\frac{m}{k}} \end{array}\end{array}\)
Yayın Esneklik Katsayısı k:
* Yapıldığı maddenin cinsine
* Yayın boyuna
* Yayın helezoniklerinin sıklığına bağlıdır
Yayın Periyodu T:
* Yay sabitine
* Asılı kütleye bağlıdır
* Fakat uzanımdan ve yerçekiminden bağımsızdır.
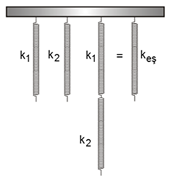
Yayların Bağlanması
* Seri Bağlama
\(\frac{1}{{{k_{eş}}}}{\rm{ = }}\frac{1}{{{k_1}}}{\rm{ + }}\frac{1}{{{k_2}}}\)
İki Yay için \({k_{eş}}{\rm{ = }}\frac{{{k_1}{\rm{.}}{k_2}}}{{{k_1} + {k_2}}}\)
Özdeş n adet yayn için \({k_{eş}}{\rm{ = }}\frac{k}{n}\)
* Paralel Bağlama
\({k_{eş}} = {k_1} + {k_2}\)
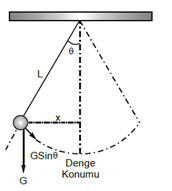
* Basit Sarkaç
\(\theta < {15^o}C\) olmak üzere hareket eden ipe bağlı cisim Basit Harmonik Hareket yapar.
Hareketlinin periyodu;
\(\begin{array}{l}Sistemi\,\,Hareket\,\,Ettiren\,\,Kuvvet\,\,;\,\,F{\rm{ = }}GSin\theta \\F{\rm{ = }}ma{\rm{ = }}mg.Sin\theta \,\,;\,\,Sin\theta {\rm{ = }}\frac{x}{L}\\\frac{{4{\pi ^2}.x}}{{{T^2}}}{\rm{ = }}g.\frac{x}{L}\\{T^2}{\rm{ = }}\frac{{4{\pi ^2}.L}}{{.g}}\\T{\rm{ = }}2\pi \sqrt {\frac{L}{g}} \end{array}\)
ile bulunur.
Hareketin Periyodu T:
* Sarkaç boyuna
* Çekim ivmesine bağlıdır.
* Fakat kütleden ve uzanmadan bağımsızdır.