Düzgün Dairesel Hareket
Dairesel bir yörünge üzerinde sabit hızlı olarak gerçekleşen dönme hareketine Düzgün Dairesel Hareket denir.
Periyot (T):
Düzgün Dairesel Hareket yapan cismin bir tam tur atması
esnasında geçen süre.
Frekans (f):
Düzgün Dairesel Hareket yapan cismin bir saniyede attığı tur sayısı.
\({\rm{T}}{\rm{.f = 1}} \Rightarrow {\rm{T = }}\frac{{\rm{1}}}{{\rm{f}}} \Rightarrow {\rm{f = }}\frac{{\rm{1}}}{{\rm{T}}}\)
Çizgisel (Teğetsel) Hız (V):
Düzgün Dairesel Hareket yapan cismin birim zamanda dairesel yörünge üzerinde aldığı yol;
\(\begin{array}{*{20}{l}}{\vartheta = \frac{{\Delta x}}{{\Delta t}}}\\{\Delta x = 2\pi r}\\{\Delta t = T}\end{array}\)
\(\vartheta {\rm{ = }}\frac{{2\pi .r}}{T}\,\,{\rm{ = }}2\pi .r.f\)
Açısal Hız (w):
Düzgün Dairesel Hareket yapan cismin birim zamanda taradığı açıya denir.
\(\begin{array}{*{20}{l}}{w{\rm{ = }}\frac{\theta }{t}}\\{\theta {\rm{ = }}2\pi {\mkern 1mu} }\\{t{\rm{ = }}T}\end{array}\)
\(w{\rm{ = }}\frac{{2\pi }}{T}\,\,{\rm{ = }}2\pi .f\)
Çizgisel hız ile açısal hız arasında v=wr ilişkisi vardır.
Merkezcil İvme (a):
Düzgün Dairesel Hareket yapan cismin birim zamanda hızında görülen değişme miktarıdır. Bu değişim büyüklük olarak gözlenmez, fakat yön olarak hız sürekli değişir.
\(a{\rm{ = }}\frac{{2\pi \vartheta }}{T}{\rm{ = }}w\vartheta {\rm{ = }}{w^2}.r{\rm{ = }}\frac{{{\vartheta ^2}}}{r} \Rightarrow a{\rm{ = }}\frac{{2{\pi ^2}}}{{{T^2}}}.r\)
Merkezcil Kuvvet (Fm):
\(F{\rm{ = }}ma{\rm{ = }}m\frac{{{\vartheta ^2}}}{r}{\rm{ = }}m.{w^2}.r{\rm{ = }}m\frac{{4{\pi ^2}}}{{{T^2}}}r\)
Düzgün Dairesel Hareket Uygulamaları
* Yatay Düzlemde Düzgün Dairesel Hareket
\(T{\rm{ = }}m.\frac{{{\vartheta ^2}}}{r}{\rm{ = }}m.\frac{{4{\pi ^2}}}{{{T^2}}}.r\)
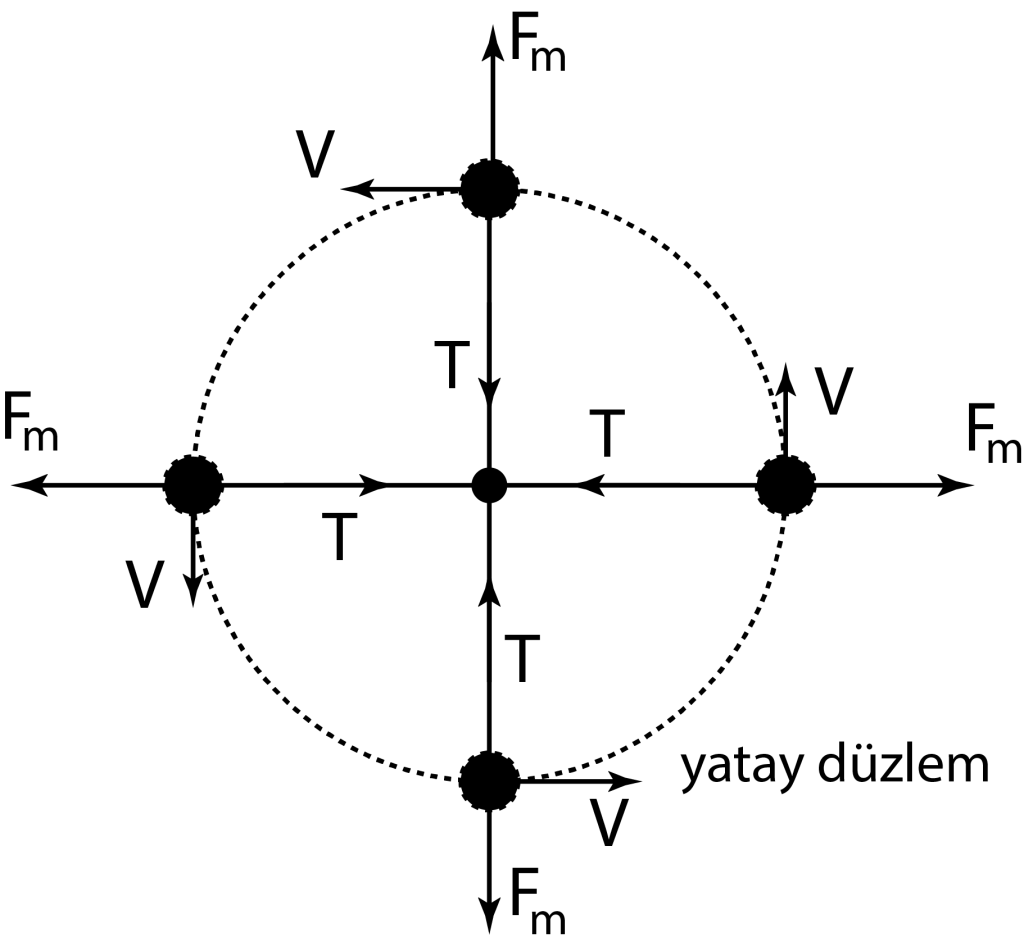
* Düşey Düzlemde Düzgün Dairesel Hareket
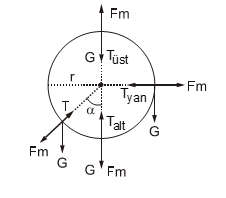
\(\begin{array}{*{20}{l}}{{T_{ust}} = {F_m} – G}\\{{T_{yan}} = {F_m}}\\{{T_{alt}} = {F_m} + G}\\{T = {F_m} + GCos\alpha }\end{array}\)
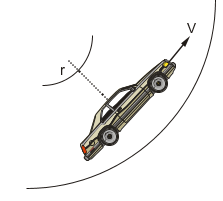
* Yatay Viraj
Viraja giren araba tekerlekleri ile yer arasındaki sürtünme sayesinde kaymadan virajı alabilir. Buna göre virajı kaymadan alabileceği en büyük hız;
\(\begin{array}{*{20}{l}}{{F_S} \ge {F_m}}\\{k.m.g \ge m.\frac{{{\vartheta ^2}}}{r}}\\{{\vartheta ^2} \le k.g.r}\\{\vartheta \le \sqrt {k.g.r} }\end{array}\)
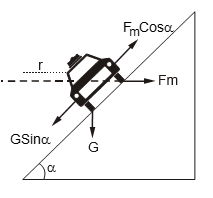
* Eğimli Viraj
Eğimli virajlarda cismin merkezkaç kuvvetini eğimden dolayı arabanın ağırlığı dengeler ve böylece sürtünmeye gerek duyulmaz. Bu durumda;
\(\begin{array}{*{20}{l}}{{F_m}Cos\alpha {\rm{ = }}GSin\alpha }\\{m.\frac{{{\vartheta ^2}}}{r}.Cos\alpha {\rm{ = }}m.g.Sin\alpha }\\{{\vartheta ^2}{\rm{ = }}r.g.\frac{{Sin\alpha }}{{Cos\alpha }}{\rm{ = }}r.g.\tan \alpha }\\{\vartheta {\rm{ = }}\sqrt {r.g.\tan \alpha } }\end{array}\)
* Rotor
Cismin düşmeden dönebilmesi için;
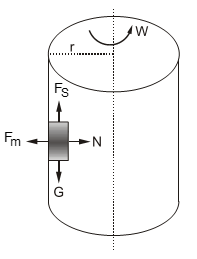
\(\begin{array}{*{20}{l}}{{F_S} \ge G}\\{{F_S}{\rm{ = }}k.N{\mkern 1mu} {\mkern 1mu} ;{\mkern 1mu} {\mkern 1mu} N{\rm{ = }}{F_m} \Rightarrow {F_S}{\rm{ = }}k.{F_m}}\\{k.m.\frac{{{\vartheta ^2}}}{r} \ge m.g}\\{\vartheta {\rm{ = }}\sqrt {\frac{{r.g}}{k}} }\end{array}\)
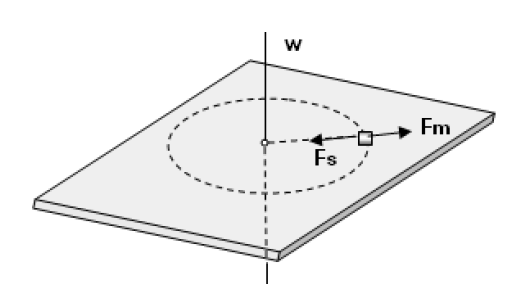
* Yatay Düzlemde Dönen Tabla:
Cismin kaymadan durabilmesi için;
\(\begin{array}{*{20}{l}}{{F_S} \ge {F_m}}\\{k.m.g \ge m.\frac{{{\vartheta ^2}}}{r}}\\{{\vartheta ^2} \le k.g.r}\\{\vartheta {\rm{ = }}\sqrt {k.g.r} }\end{array}\)