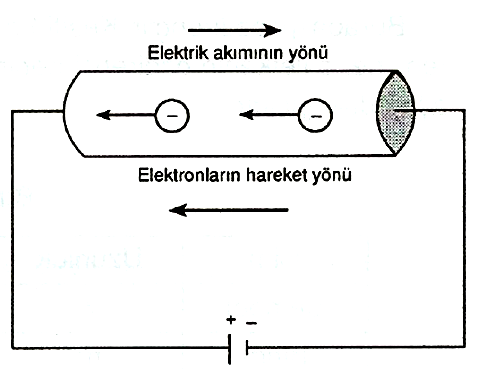
Elektrikle yüklü ve potansiyelleri farklı olan iki iletken küreyi, iletken bir telle birleştirirsek, potansiyel farkından dolayı iletkende yük akışı meydana gelir. Bir iletkenden uzun süreli elektrik yükü akışını sağlamak için, iletkenin iki ucu arasında sürekli bir potansiyel farkı oluşturmak gerekir. Bunu da pil, batarya, akümülatör vb. düzeneklerle sağlayabiliriz.
Elektrik Akım Şiddeti
İletken bir ortamın herhangi bir kesitinden belirli bir yönde, birim zamanda geçen elektrik yükü miktarına elektrik akım şiddeti denir. “i” ile gösterilir. Buna göre bir iIetkenin herhangi bir kesitinden t sürede q kadar net yük geçiyorsa, iletkenden geçen akım şiddeti
\(i = \frac{q}{t}\)
olur.
| Yük (q) | Zaman (t) | Elektrik Akımı (i) |
| Coulomb (C) | Saniye (s) | Coulomb/saniye (C/s)Amper (A) |
Pozitif (+) Elektrik yüklerinin hareketi; potansiyeli yüksek o|lan noktadan, potansiyeli düşük olan noktaya doğrudur. Elektrik akımının yönü, pozitif (+) yüklerin hareket yönü olarak veya elektron hareketinin zıt yönünde kabul edilir. İletken metallerde elektrik akımı, serbest hareket edebilen elektronlarla sağlanır.
Bir İletkenin Direnci
Bir iletkenin, yük akışına (metallerin ise elektron akışına) karşı koymasına direnç denir.Bir iletkenin direnci:
1. Uzunluğu (l) ile doğru orantılıdır.
2. Kesit alanı (A) ile ters orantılıdır.
3. Öz direnci (\(\rho \)) ile doğru orantılıdır.
Buna göre direnç :
\(R = \rho \cdot \frac{\ell }{A}\)
Burada (\(\rho \)) öz dirençtir. Kesiti 1m2 olan bir iletkenin, bir birim boyunun (1m) direncine, öz direnç denir. Maddenin cinsini ifade eder. Birim tablosu aşağıdaki gibidir.
| İsim | Uzunluk | Kesit | Öz Direnç | Direnç |
| Sembol | \[\ell \] | \[A\] | \[\rho \] | \[R\] |
| Birim | m | m2 | \[\Omega \cdot m\]\[Ohm \cdot m\] | \[\Omega \]Ohm |
Not: Öz direncin tersine elektriksel iletkenlik denir. Gümüş, bakır ve altın, iletkenliği en yüksek metallerdir. Ancak gümüş ve altın pahalı olduğundan, iletken olarak en çok bakır kullanılmaktadır.
Direncin Sıcaklıkla Değişimi
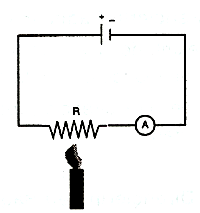Bir elektrik devresindeki devre elemanları, elektrik akımının etkisiyle veya dış etkilerle ısınırsa dirençleri artar ve devreden geçen akım şiddeti zamanla azalır.
Bir iletkenin direnci sıcaklıkla;
\(\Delta R = {R_0} \cdot \alpha \cdot \Delta T\)
kadar değişir. Bu durumda iletkenin direncinin sıcaklığa bağlı ifadesi
\(R = {R_0} + {R_0} \cdot \alpha \cdot \Delta T\)
eşitliğiyle verilir. Burada, R0 iletkenin T0 sıcaklıktaki direnci; \(\alpha \) ise direncin sıcakIıkla değişim katsayısıdır. (birimi 1/°C)
Not: Metaller soğutulursa dirençleri azalır.Mutlak sıfır (0°K = -273°C) sıcaklıkta bazı metaller süper iletken hale gelir. (Alüminyum, kalay, kurşun, çinko gibi)
Ohm Kanunu
Bir iletkenin iki ucu arasındaki gerilimin (potansiyel farkının) iletkenden geçen akım şiddetine oranı sabittir. Bu sabit değere, elektriksel direnç ya da direnç denir.
Buna göre bir iletkenin direnci:
\(R = \frac{V}{i}\)
ile verilir. Bu oranı ilk defa George Simon Ohm (1789- 1854) bulduğu için bu bağıntıya Ohm Kanunu denmiştir.
| Potansiyel Fark (v) | Akım Şiddeti (i) | Direnç (R) |
| Volt (v) | Amper (A) | Ohm (\(\Omega \)) |
Dirençler elektrik devrelerinde,
şeklinde gösterilir.
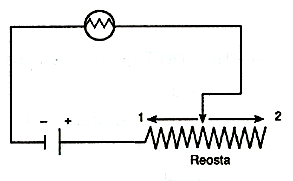
Değişken (ayarlanabilen) dirençlere Reosta denir. Reosta sürgüsü 1 yönünde hareket ettirilirken devrenin toplam direnci azalır. Üretecin emk değeri sabit ve direnç ile akım ters orantılı olduğundan devrede dolaşan akım şiddeti ve dolayısıyla lambanın parlaklığı artar.
Akım Şiddetinin ve Potansiyel Farkının Ölçülmesi
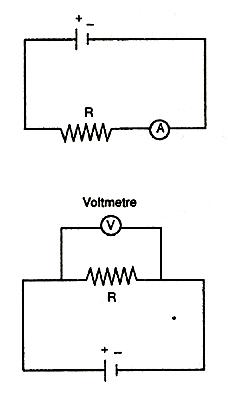Elektrik akım şiddeti Ampermetre ile, iki nokta arasındaki potansiyel fark ise Voltmetre ile ölçülür. İki ucu arasındaki potansiyel farkı ve üzerinden geçen akım şiddeti bilinen bir devre elemanının direnci de Ohm Kanununa göre bulunabilir. Bir devre direnci Ohmmetre denen bir cihazla da ölçülebilir.
Ampermetre devreye seri bağlanır. Devre akımını etkilememesi için, ampermetrenin direncinin çok küçük (mümkünse sıfıra yakın) olması gerekir. Bu nedenle Ampermetrenin direnci ihmal edilir.
Voltmetre ise potansiyel farkı ölçülecek noktalar arasına paralel olarak bağlanır. Üzerinden akım geçmemesi için direncinin çok büyük olması gerekir.
Dirençlerin Bağlanması
Elektrik devrelerinde dirençleri seri ya da paralel bağlayarak, uygulamada ve teoride bazı kolaylıklar sağlanır. Birden çok direncin yaptığı etkiyi tek başına yapabilen dirence eşdeğer direnç denir.
1. Dirençlerin Seri Bağlanması
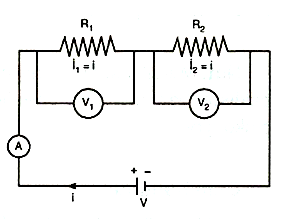
Dirençlerin aynı akım yolu üzerinde olacak şekilde uç uca eklenmeleriyle oluşan bağlanma şeklidir. Şekildeki R1 ve R2 dirençleri seri bağlanmıştır. A ampermetresinden geçen akım, R1 ve R2 dirençlerinden aynen geçer. Buna göre seri bağlı dirençlerden geçen akımlar birbirine eşittir.
– \(i = {i_1} = {i_2} = …\)
Dirençlerin uçları arasındaki potansiyel fark sistemi besleyen üretecin gerilimine eşittir.
– \(V = {V_1} + {V_2} + …\)
Devrenin eşdeğer direnci, direnç büyüklüklerinin aritmetik toplamına eşittir.
– \({R_{es}} = {R_1} + {R_2} + …\)
Not: Seri bağlı direnlerin uçları arasındaki gerilim dirençlerin büyüklükleri ile doğru orantılıdır.
Dirençlerin Paralel Bağlanması
İki yada daha fazla direncin, birer uçların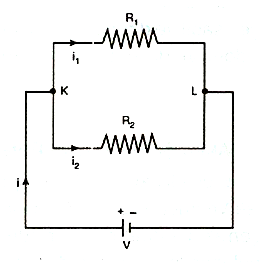
ın kendi aralarında birleştirilmeleri ile oluşan bağlama şeklidir. Üreteçten çıkan ana kol akımı, düğüm noktasında (K bağlantı noktasında) direnç sayısı kadar kola ayrıIır. Bu durumda paralel bağlı dirençlerde;
Ana koldan gelen akım paralel bağlı dirençler üzerinden geçerken, direncin büyüklüğüyle ters orantılı olarak dağılır. Böylece dirençler üzerinden geçen akımların toplamı, ana koldan geçen akıma eşit olur:
– \(i = {i_1} + {i_2} + …\)
Dirençlerin ve üreteçlerin birer uçları aynı noktaya bağlı olduğundan paralel kolların gerilimi üretecin gerilimine eşittir.
– \(V = {V_1} = {V_2} = …\)
Devrenin eşdeğer direnci;
\(\frac{1}{{{R_{es}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + …\)
Yukarıdaki bağıntıdan paralel bağlı iki direnç için;
\({R_{es}} = \frac{{{R_1} \cdot {R_2}}}{{{R_1} + {R_2}}}\)
Not: n tane özdeş direnç paralel bağlı ise;
\({R_{es}} = \frac{R}{n}\)
