Heisenberg Belirsizlik İlkesi

Elektron gibi bir taneciğin nerede olduğu kesin olarak biliniyorsa, aynı anda taneciğin nereden geldiği veya nereye gittiğini kesin olarak bilemeyiz. Benzer şekilde, taneciğin nasıl hareket ettiğini biliyorsak onun konumunu kesin olarak bilemeyiz.

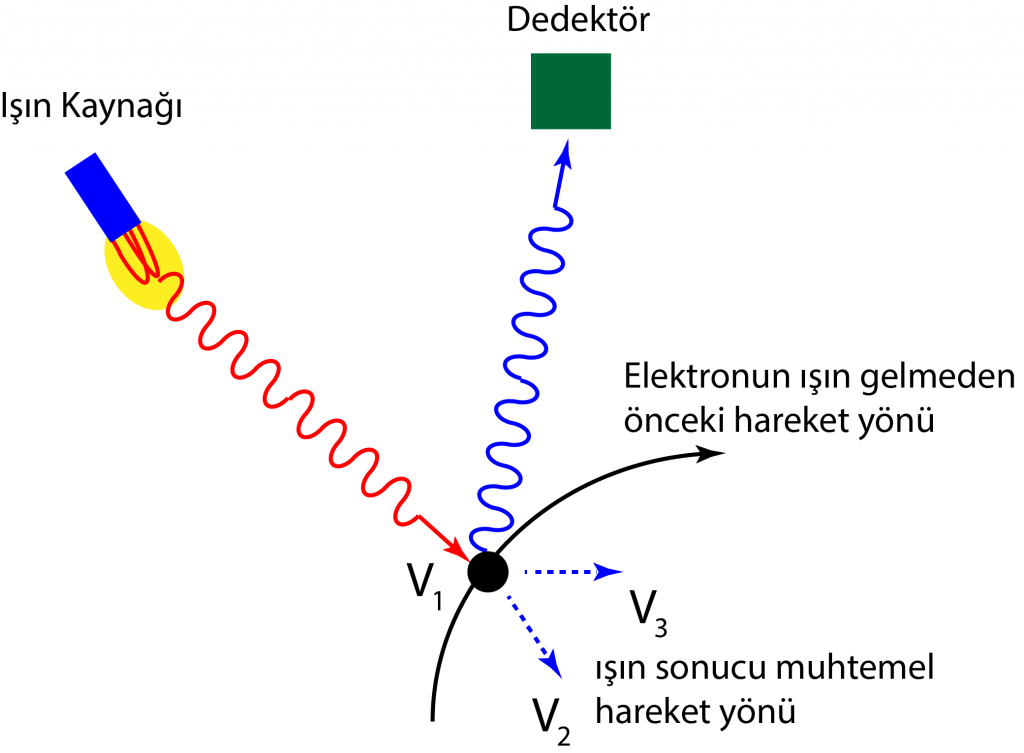
Elektronun herhangi bir andaki konumu ve momentumu aynı zamanda kesin olarak bilinemez. Bir taneciğin yerini ve momentumunu belirlemek için, o taneciği görmek gerekir. Taneciğin görünmesi ise taneciğe ışın dalgası göndermek ile olur. Elektron gibi küçük taneciklerin konumunu belirlemek için gönderilen uygun dalga boyundaki ışın elektrondan yansıdığında elektronun anlık konumu belirlenir. Fakat gönderilen ışın elektronun konumunu ve momentumunu değiştirir.

Işın gönderilerek anlık konumu belirlenen elektronun, ışının elektrona enerji aktarmasından dolayı yönünde ve momentumunda değişme olduğu için etkileşimden önceki momentumu belirsizdir ve bilinemez.

Eğer bir parçacığın konumu Δx duyarlılığı ile ve momentumunun ölçümü de ΔP duyarlılığı ile yapılırsa, iki belirsizliğin çarpımı asla $\frac{h}{{4\pi }}$ mertebesinde bir sayıdan daha küçük olamaz.

$\begin{array}{l} \Delta x \cdot \Delta P \ge \frac{h}{{4\pi }}\\ \Delta x \cdot \Delta P \ge \frac{\hbar }{2}\\ (\hbar  = \frac{h}{{2\pi }}) \end{array}$

Sonuç olarak elektronun çekirdek etrafında belirli dairesel yörüngeler izledikleri deneysel olarak ispatlanamaz. Yani Bohr’un dediği gibi elektronların dairesel hareket yaptığı ispatlanamaz. Ancak yörünge yerine elektronun (ya da elektronların) çekirdek etrafında bulunma olasılığının olduğu bölgelerden söz edilebilir. Heisenberg’in belirsizlik ilkesi bize, ışık ve maddenin dalga-tanecik ikili doğasını daha iyi anlamamızı sağlar.  Eğer bir elektronun parçacık özelliğini ortaya çıkarmak için bir deney düzenlenirse, onun dalga özelliği daha az ortaya çıkacaktır. Benzer şekilde, eğer deney, elektronun dalga özelliğini hassas olarak ölçmek için düzenlenirse, onun tanecik özelliği daha az görünür.

Heisenberg aynı zamanda enerji-zaman belirsizliğine de işaret etmiştir. Bu belirsizlik; bir parçacığın enerjisinin sonlu bir ölçüm süresi içerisinde tam olarak ölçülemeyeceğini vurgular. Buna göre;

$\begin{array}{l} \Delta E \cdot \Delta t \ge \frac{h}{{4\pi }}\\ \Delta E \cdot \Delta t \ge \frac{\hbar }{2}\\ (\hbar  = \frac{h}{{2\pi }}) \end{array}$

sonucuna ulaşılır.

ΔE: Enerji ölçümündeki belirsizlik

Δt: Zaman ölçümündeki belirsizlik