Modelleme ve Matematik
Modelleme, ayrıntıları yeterince bilinmeyen bir olayı, bilinen olaylar ya da bilgiler ışığında daha anlaşılır ve basit hale getirmektir. Aslında gerçeğe benzer görüntüler oluşturmaktır.

İlk çağlarlardan bu yana insanlar karşılaştıkları problemleri çözmeye, doğayı anlamaya ve ona hakim olamaya ya da rahat ve güvenli yaşamak için sistemin kendisi ya da modeli üzerinde gözlem veya deneyler yapma ihtiyacı hissetmişlerdir.
Modelleme ile,
– Mekanizması bilinmeyen olayların daha anlaşılır hale gelmesi,
– Hipotezlerin test edilmesi
amaçları güdülür.
Modelleme yapmadan önce modellenecek olay ya da olgunun iyi gözlenmesi gerekir. Modelleme yapmadan önce
modellenecek sistem,
Yeterince gözlenmeli,
Modellenecek sistemin başka sistemlerle ilişkileri incelenmeli,
Dış görünüşü (renk, koku, şekil) bilinmeli,
Yukarıdaki işlemlerden sonra modellenecek sistemle ilgili kurallar belirlenmeli.
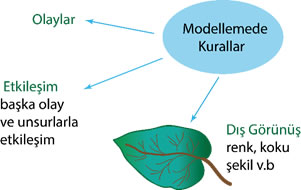
Yapılan gözlemler sonucu elde edilen kurallar;
– Sistem üzerinde oluşan olayları,
– Başka sistemlerle olan etkileşimleri,
– Sistemin dış görünüşünü
kapsamalıdır.
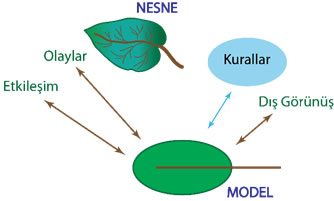
Bir model, gerçek sistemle ilgili olayları, etkileşimleri, gerçek sistemin dış görünüşünü ve bunlarla elde edilen sistemin genel kurallarını kapsar.
Fizik, doğal olayları doğru ve yeterli açıklayabilmek için modellemeden yararlanır. Modelleme sayesinde gerçek olaylarla ilgili yapılabilecek deney ve gözlemler daha rahat ve daha az zaman kaybedilerek gerçekleştirilebilir. Ancak modelleme olayın sadece bir yönüyle ilgili olabilir, dolayısıyla kompleks bir olay için tek bir model yeterli gelmeyebilir.
Modeller kullanılırken, onların sadece gerçeğin kopyaları olduğu ve gerçeği açıklamak için araç olduğu unutulmamalıdır. Asla gerçeğin kendisi ile karıştırılmamalıdır.
Fizik, modelleri genellikle Matematik dili ile ifade eder. Ancak elde edilen matematiksel sonuçların öncelikle gerçek sistemler üzerinde kontrol edilmesi gerekir.
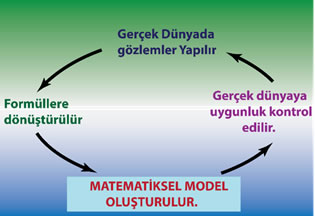
Gerçek dünyada yapılan gözlemler, formüllere dönüştürülerek matematiksel modeller oluşturulur.
Oluşturulan matematiksel modeller gerçek dünyada kontrol edilerek uygunsa kullanılır, eğer değilse gözlemler tekrarlanarak aynı işlemler tekrarlanır.
Örnek
Bir kenarı a olan bir karenin alanı A=4m2 olsun. Karenin alan formülü A=a2 kullanı-larak a değeri +2 ve -2 olarak bulunur.

Ancak uzunluk değeri negatif değer alamaz. Yani matematiksel ifadelerle elde edilen sonuçlar gerçekle uyumlu olmalıdır. Bu nedenle pozitif olan sonuç bizim için doğrudur.
Bilimsel Yasalar ve teoriler,
Matematiğin yardımıyla deneylerden elde edilen sonuçlarla fiziksel büyüklükler ilişkilendirilirler. Yasalar genellikle matematiksel formüllerle ifade edilirler. Teoriler ise olaylar karşısında oluşturulmuş deney ve gözlemlere dayalı açıklamalardır.