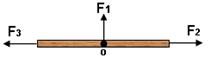
Tork: Kuvvetin döndürücü etkisine moment (Tork) denir.
Vektörel bir büyüklüktür. \(\tau \) ile gösterilir. Kuvvet yada kuvvetin doğrultusuna dik uzaklığın çarpımına eşittir.
Moment (Tork), uygulanan kuvvet ile doğru orantılıdır.
Moment (Tork) kuvvetin doğrultusunun dönme eksenine olan uzaklığıyla da doğru orantılıdır.
Bu iki orantıyı düzenlersek ;
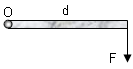
\(\tau = F \cdot d\)
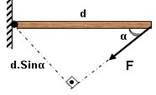
Bir cismi döndürmek için uygulanacak kuvvet, uygulama noktası ile dönme noktasını birleştiren doğruya dik olmalı veya bu doğruya dik bileşeni bulunmalıdır.
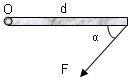
\(\tau = F \cdot d \cdot Sin\theta \)
Tork iki yolla bulunabilir.
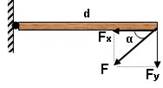
a ) Tork= ( dik kuvvet ) x uzaklık
\(\tau = (F \cdot Sin\theta ) \cdot d\)
b ) Tork = kuvvet x ( dik uzaklık )
\(\tau = F \cdot (d \cdot Sin\theta )\)
Eğer bir kuvvetin uygulama noktası dönme noktası ise yada kuvvetin doğrultusu dönme noktasından geçiyorsa o kuvvetin momenti sıfırdır yani döndürme etkisi yoktur. d = 0 olduğu için,tork=0 ‘dır.
Toplam tork ve Toplam Dönme Yönü
Bir cisme aynı düzlemde etkiyen kuvvetlerin oluşturduğu momentlerin toplamını bulmak için bir yön (+), diğer yön (-) seçilir. Genellikle saat yönü (-) seçilir
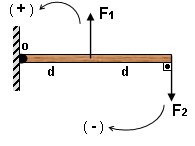
\(\begin{array}{*{20}{l}}{{\tau _1} = {F_1}d}\\{{\tau _2} = {F_2}2d}\\{\sum \tau = {F_1}d – {F_2}2d}\end{array}\)
Sonuç (-) çıkarsa, negatif yönde döner. Sonuç (+) çıkarsa, pozitif yönde döner.
Sonuç sıfır çıkarsa cisim dönmez veya kuvvetler uygulanmadan önceki hareket durumunu devam ettirir.
KESİŞEN KUVVETLERİN DENGESİ
Bir cisim üzerine etki eden kuvvetlerin dengesi demek; Bileşke Kuvvetin “0” (Sıfır) olması demektir.
\({\overrightarrow F _{Net}} = 0\)
Kuvvet dengesinin açacak olursak;
\(\sum {{{\overrightarrow F }_X}} = 0\)
\(\sum {{{\overrightarrow F }_y}} = 0\)
Lami Teoremi (Sinüs Teoremi)
Kesişen üç kuvvet dengede ise;

* Kuvvetlerin karşılarındaki açıların sinüslerine oranı sabittir.
\(\frac{{{F_1}}}{{Sin\alpha }} = \frac{{{F_2}}}{{Sin\theta }} = \frac{{{F_3}}}{{Sin\beta }}\)
* Küçük açı karşısında büyük kuvvet, büyük açı karşısında küçük kuvvet bulunur.
\(\alpha > \beta > \theta \) ise
\({F_2} > {F_3} > {F_1}\)
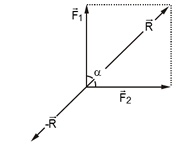
Dengeleyici Kuvvet
Yönce bileşke kuvvete ters, fakat büyüklüğü eşit olan kuvvete denir. Dengeleyici kuvvet \( – \overrightarrow R \) ’dir.